달콤하게 즐기자, 초콜릿 수학

지난 2월 14일은 온 세계가 달콤하게 물드는 밸런타인데이였다. 기독교 사제인 성 발렌티누스를 기념하는 날로, 서양에서는 성별에 상관없이 선물을 주고받거나 연인과 로맨틱한 하루를 보낸다. 사실 그 유래로 볼 때는 초콜릿과 별다른 연관이 없으나 우리나라를 비롯한 일본, 중국 등에서는 초콜릿을 주고받는 날이라는 인식이 강하다. 상술에 지는 것 같기도 하지만, 이런 핑계로 마음껏 디저트를 먹는 것 또한 좋은 기회가 아닌가. 그래서 오늘은 초콜릿 선물에 곁들이기 좋은 쉽고 재미있는 ‘초콜릿 수학’ 문제들을 준비했다.

초콜릿 먹는 횟수로 상대방 나이 알아내기

일주일에 초콜릿을 10번 이상 먹는 초콜릿 중독자가 아니라면 누구나 해볼 수 있는 간단한 수학 마술이 있다. ‘초콜릿 수학’으로 불리는 이 문제는 초콜릿 먹는 횟수를 이용해 상대의 나이를 알아내는 계산법이다. 질문들에 대답해 보고 원리를 생각해 보자.

1. 지난 1주일 동안 며칠이나 초콜릿을 먹었는지 생각하시오(1~9 사이의 수 중 선택).

2. 그 숫자에 2를 곱하시오.

3. 그 숫자에 5를 더하시오.

4. 2의 결괏값에 50을 곱하시오.

5. 올해 생일이 지나갔다면 1770을, 아직 지나지 않았다면 1769를 더하시오.

6. 4의 결괏값에 태어난 연도를 빼시오.

6번까지 계산을 마치면 세 자릿수를 얻는다. 이때 첫 번째 수는 1번에서 답했던 초콜릿을 먹은 횟수, 나머지 두 수는 참여자의 만 나이다.

어린아이라면 깜짝 놀라겠지만 성인이라면 아마 이와 비슷한 식의 수학 마술을 접한 경험이 한 번쯤은 있을 것이다. 하지만 어떤 원리로 답을 찾는지까지 분석해 본 사람은 적을 것이다. ‘초콜릿 수학’의 증명은 다음과 같다.

처음 초콜릿 먹은 횟수로 고른 값을 x라고 하면 각 단계에서 숫자는

1. x

2. 2x

3. 2x+5

4. 50(2x+5)

5. 50(2x+5)+1770 or 50(2x+5)+1769

6. 50(2x+5)+1770-(2020-10T-W) or 50(2x+5)+1769-(2020-10T-W-1)

이 된다. 6번 식을 전개해서 정리하면 생일이 지났든 지나지 않았든 계산 결과는 100x+10T+W로 구해진다. 따라서 x는 백의 자릿수, T는 십의 자릿수, W는 일의 자릿수며, 1번과 6번에서 자신이 제공한 숫자에 의해 항상 모든 참여자는 초콜릿 먹은 횟수와 나이를 결괏값으로 얻게 된다. 비슷한 유형의 수학 마술들도 미지수를 이용해 다항식을 세워 보면 원리를 금방 파악할 수 있다.

무한 초콜릿 패러독스

이번엔 수학 실험도 겸할 수 있는 재미있는 초콜릿 패러독스를 살펴보자. 이는 한때 인터넷을 돌며 네티즌을 뜨겁게 달구고 진실 여부로 머리를 싸매게 했던 문제다. 제목부터가 흥미로운 ‘무한히 초콜릿 먹는 법’이다. 아래 그림을 따라 방법을 확인해 보자.

출처: pinterest

가로 다섯 칸, 세로 다섯 칸 판 초콜릿에서 시작한다. 먼저 대각선으로 자르고 잘린 조각의 윗부분을 세로로 자른다(❶). 그다음 잘린 왼쪽 조각을 한 번 더 가로로 자르고(❷) 오른쪽 조각과 왼쪽 조각의 자리를 바꾼다(❸). 남는 공간에 ❷번 과정에서 생긴 작은 조각을 붙인다(❹). 직사각형 모양을 완성하면 초콜릿 한 칸이 넘친다. 이 부분을 잘라 낸다(❺). 잘라 낸 한 칸을 먹는다. 다시 초콜릿을 세어 본다. 초콜릿은 여전히 가로 다섯 칸 세로 다섯 칸이다. 따라서 ❶~❺번 과정을 무한히 반복하면 계속 초콜릿 한 칸씩을 먹으면서 초콜릿을 보존할 수 있다.

질량과 부피가 주어진 물질을 아무리 잘라 내도 같은 상태로 보존된다는 것은 상식적으로 말이 안 된다. 그러나 그림에서는 물론이고 실제 초콜릿을 가지고 실험해 봐도 정말 칸수가 동일하다는 것을 확인할 수 있다. 초콜릿으로 식량난을 해결할 수 있는 시대가 온 걸까? 비결은 다음과 같다.

무한 초콜릿 문제는 기하학적 오류를 이용한 ‘패러독스 퍼즐’이다. 패러독스 퍼즐은 ‘잃어버린 사각형 퍼즐’이라고도 불리며, 사람의 눈으로 쉽게 알아차리기 힘든 기하학적 눈속임을 이용해 모순을 일으킨다. 초콜릿을 칼로 자르면 아무리 정교해도 경계면이 아주 매끄러울 수는 없는데, 이 때문에 사람들은 조각을 옮기고 붙이면서 발생한 틈새의 변화를 쉽게 눈치채지 못한다.

출처: 위키미디어

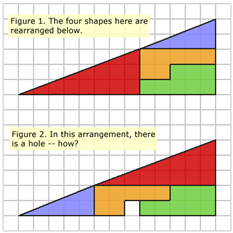
또 다른 패러독스 퍼즐 예시를 보자. 위 그림은 첫 번째 삼각형의 조각을 그대로 옮겨 두 번째 삼각형을 만든 모양이다. 위 삼각형은 가로 13칸, 세로 5칸이고 아래 삼각형 역시 가로 13칸, 세로 5칸이다. 같은 조각 같은 면적이니 딱 맞게 채워져야 하는데 아래 삼각형에 한 칸의 남는 공간이 생긴다.

귀신이 곡할 노릇이지만 눈을 씻고 살펴보면 빗변의 기울기가 조금 다르다는 것을 눈치챌 수 있다. 위 삼각형은 살짝 안쪽으로 오목하고 아래 삼각형은 살짝 볼록한 빗변을 가졌다. 배경의 모눈종이를 이용해 기울기를 구해 보면 차이를 쉽게 알 수 있다. 알고 보면 무척 간단하지만, 막상 초콜릿과 같은 실제 물질로 볼 때는 거의 구분되지 않는다.

무한 초콜릿 문제 역시 이와 같은 기하학적 눈속임을 차용한다. 실제로 세로 길이를 재면서 과정을 반복하면 세로가 조금씩 줄어드는 것을 확인할 수 있다. 당연히 세 번째, 네 번째 반복하다 보면 이런 변화가 눈에 띌 것이다. 그러나 사람 눈으로 가늠하기 힘든 한 단계 정도를 진행했을 때는 영락없는 ‘무한 초콜릿’으로 보이고 만다. 오류에 빠지지 않기 위해서는 겉으로 드러나 보이는 모양에 현혹되지 않고 기울기나 길이 같은 기하학적 본질을 따져 보면 된다. 수학적 이성은 진실을 왜곡하는 법이 없으니 말이다.

밸런타인데이가 지나갔다고 아쉬워하거나 한시름 놓을 여유는 없다. 날이란 날은 모두 챙겨 우리의 주머니를 노리는 상업계의 또 다른 빅 이벤트, 화이트데이가 다가오고 있으니. 사탕도 좋고 초콜릿도 좋지만 평범하게 디저트만 건네는 대신 초콜릿 퍼즐 마술이라도 선보이면 훨씬 더 달콤한 기념일이 되지 않을까.

박현선 기자 | tempus1218@donga.com

동아사이언스 <수학동아>에서 수학 기사를 쓴다. 사람들이 싫어하는 ‘수학’이란 학문을 어떻게 하면 즐겁게 전할 수 있을지 고민하며 나날을 보내고 있다.