안녕하세요. 공부를 좋아하는 습관을 만들어 주는 아이스크림 홈런입니다.
5학년 1학기 수학 시리즈, 이번 시간엔 약분과 통분에 대해 알려드릴게요.
초등수학, 5학년 1학기 수학 목차>
약분과 통분은 예시로 시작해볼까요?
, 
, 
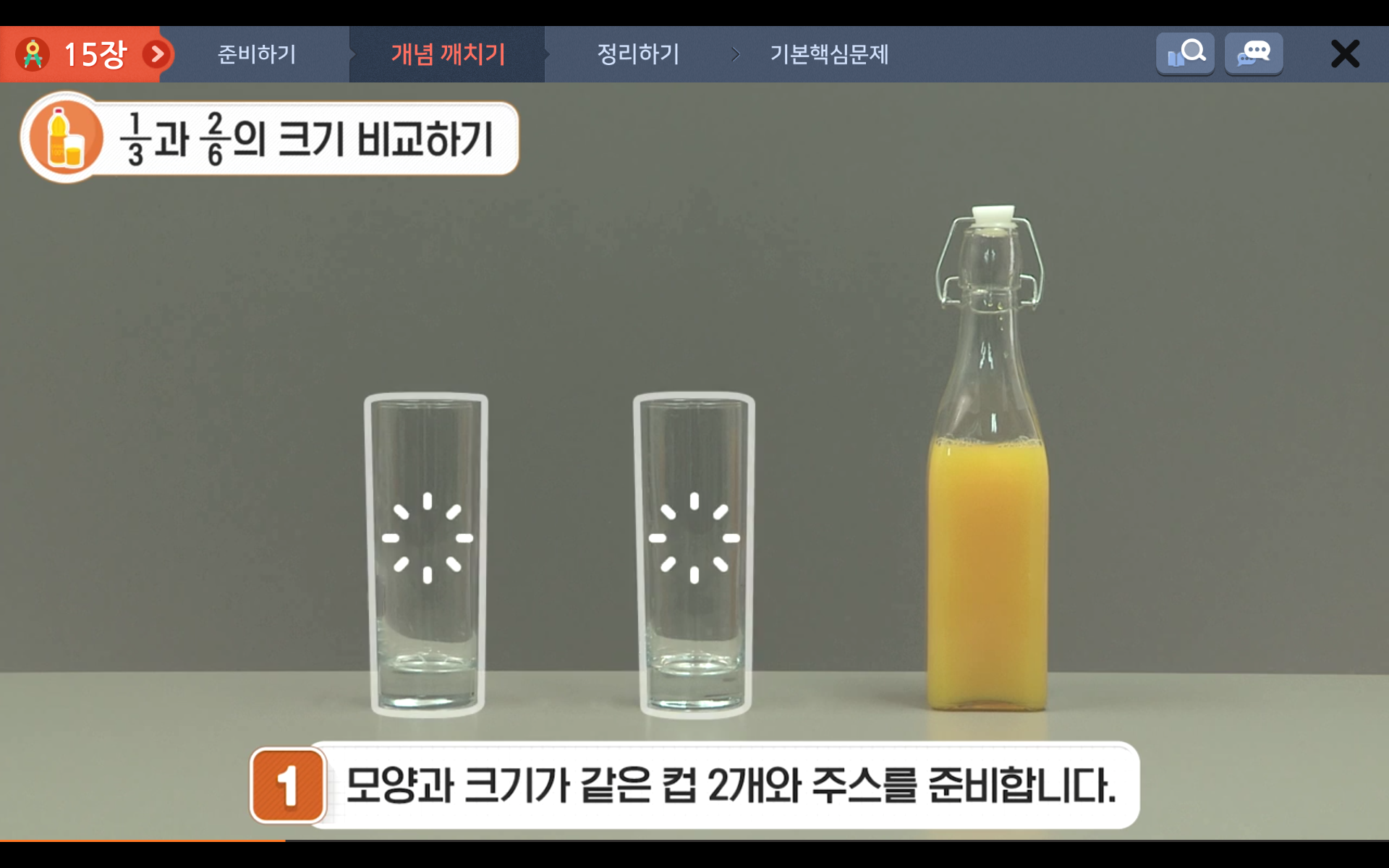
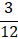은 크기가 같은 분수일까요? 다른 분수 일까요?
와 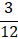를 약분하면 이 되므로,
위 세 분수는 모두 같은 분수임을 알 수 있습니다.
분모와 분자에 각각 0이 아닌 수를 곱하면 같은 크기의 분수가 되는데요,
위 숫자를 다시 볼까요?
의 분모와 분자에 각각 2를 곱해주면 가 되고, 의 분모와 분자에 각각 3을 곱해주면 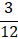이 되는걸 확인할 수 있습니다.
같은 수를 곱했을 때 같은 분수면 같은 수로 나눴을 때도 같은 분수가 되는 걸 확인할 수 있습니다.
예시를 볼까요?
,
,
도
를 분모와 분자를 각각 4로 나누면
이 되고,
를 2로 나누면
이 되므로 3개의 분수는 모두 같은 분수임을 알 수 있습니다.
이처럼 같은 수로 나누는 것을 '약분한다' 라고 합니다.
약분이란 분모와 분자를 그들의 공약수로 나누는 것 입니다.
를 분모와 분자를 각각 4로 나누어 로 만든 것을 '약분한다'라고 하는거죠.
기약분수란 분모와 분자의 공약수가 1뿐인 분수 입니다.
따라서, 분모와 분자를 그들의 최대공약수로 나누면 기약분수가 됩니다.
기약분수 하는 법은 분모와 분자를 그들의 최대공약수로 나누면 됩니다.
즉, 분모와 분자를 각각 같은 수로 나눠서 1이 아닌 다른 수로 더 이상 나눠지지 않게 해주면 됩니다.
문제로 풀어볼까요?
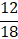을 기약분수로 나타낸다면
공약수가 1인 분수로 만들기 위해 분모와 분자가 1이 아닌 다른 수로 더 이상 나눠지지 않도록 숫자를 만들어 주면 됩니다.
즉, 분모와 분모를 각각 같은 수로 나눠서 1이 아닌 다른 수로 더 이상 나눠지지 않도록 만들어 주면 됩니다.
은 6으로 나누면 
가 되며, 2와 3은 공통인 수가 1뿐이므로, 을 기약분수로 나타내면 가 됩니다.
통분이란 분수의 분모를 같게 하는 것입니다.
공통분모란 분수의 값이 바뀌지 않고 분모의 값을 같게 한 수를 공통분모라고 합니다.
과 
로 공통분모를 만들어볼까요?
위 두 수를 통분해라 라고 하면,
가장 쉬운 방법은 서로의 분모끼리 곱해주는 거예요.
의 분모와 분자에 4를 곱하고, 의 분모와 분자에는 6을 곱해주는 거예요.
또다른 방법으로는 두 분모의 최소공배수를 공통분모로 하여 통분하는 건데요,
지난 시간에 최소공배수에 대해 배웠었죠? 최소공배수 설명한 번 더 보고 싶다면 (최소공배수 설명 보기)를 클릭해주세요.
6과 4의 최소공배수는 12이므로 에는 각각 2를 곱해주고, 에는 각각 3을 곱해주면 됩니다.
분수의 개념이 익숙해지기도 전에 약분과 통분에 대해 이해하려고 하니 헷갈릴 수 있어요.
차분히 예제 문제를 접해서 풀다 보면 약분과 통분도, 쉽게 척척 풀 수 있게 됩니다.
아이스크림 홈런 학습자료실에서 약분과 통분에 대한 보다 자세한 설명을 확인할 수 있어요!
약분과 통분 설명 더 보기>
홈런학습기로 약분과 통분 예시문제를 풀어보고 싶다면, 무료체험 해보세요!
무료체험 바로가기>
