다각형의 둘레와 넓이 | 5학년 1학기 수학 6단원 | 홈런초등

안녕하세요. 공부를 좋아하는 습관을 만들어 주는 아이스크림 홈런입니다.
5학년 1학기 수학 목차의 마지막 다각형의 둘레와 넓이에 대해 설명해드릴게요.

초등학교 5학년 수학공부 쉽고 재미있게 하는 방법>



도형이라고 하면, 이유 없이 어려울 것 같은 느낌이 들 수 있지만,
아이스크림홈런과 함께 공부하면 즐기면서 하실 수 있을 테니 포기하지 말고 함께 시작해볼까요?

가장 기본이 되는 사각형부터 스타트!
 

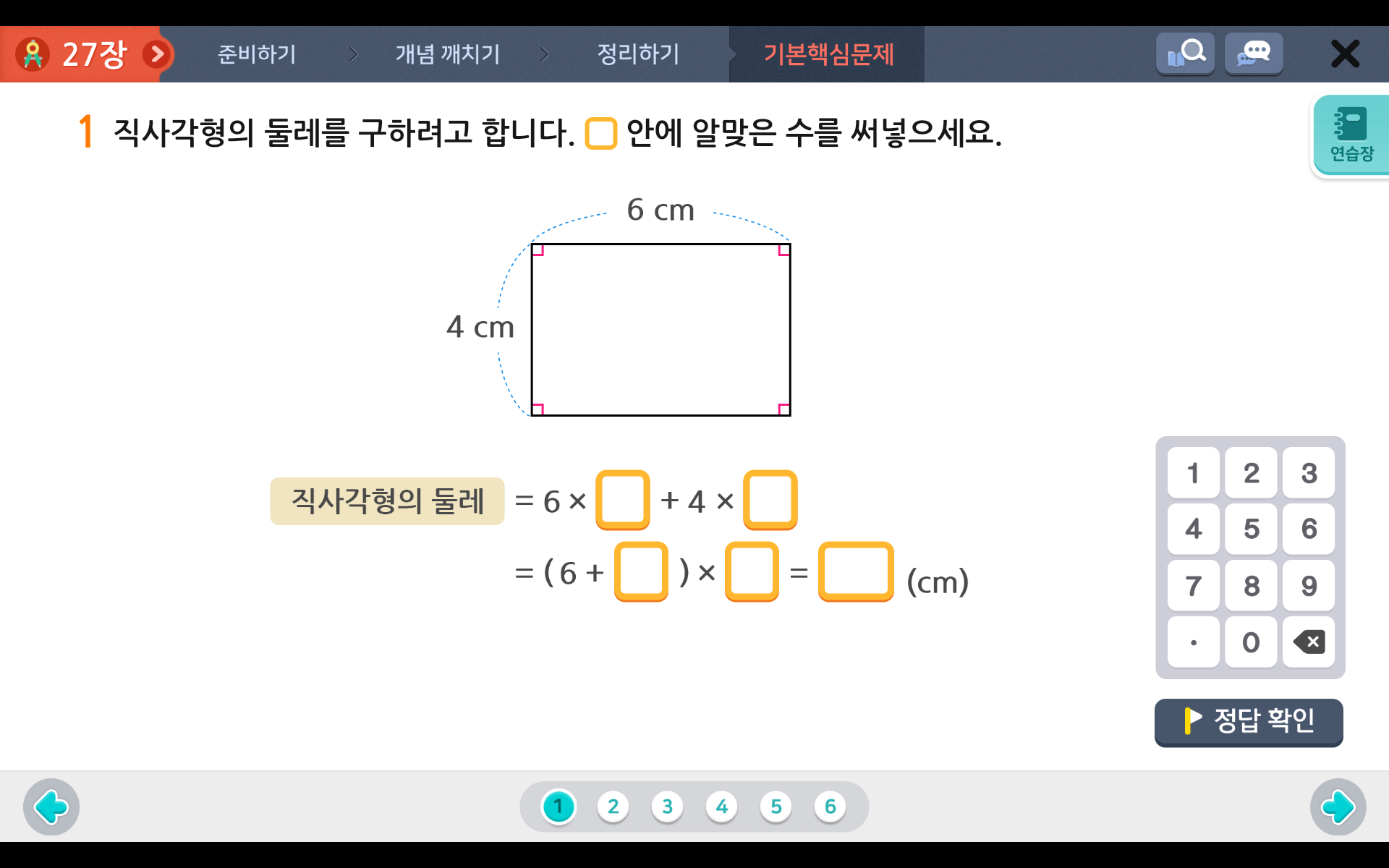
1. 직사각형 둘레: (가로 X 2) + (세로 X 2) 로 (가로 + 세로) X 2

직사각형은 마주 보는 변의 길이가 각각 같은 사각형으로, 위 직사강형 둘레 공식에 따라 가로 6, 세로 4인 직사각형의 둘레를 계산해볼까요?
(6 x 2) + (4 x 2) 또는 (6+4)x2로 20cm가 됩니다! 

 

2.평행사변형 둘레: (한 변의 길이 X 2) + (다른 한 변의 길이 X 2)

직사각형 둘레의 표현과 동일하게 (한 변의 길이 + 다른 한 변의 길이) X 2로 쓸 수 있습니다.

직사각형 및 평행사변형 둘레 구하는 문제풀기>
 

3.마름모의 둘레: 한 변의 길이 X 4 입니다.

마름모는 네 변의 길이가 모두 같지만 직각을 이루지 않는 사각형으로, 만약 한 변의 길이기 7인 마름모의 둘레를 구한다면, 
위 공식에 따라 한 변의 길이인 7 x 4 이므로 28cm 임을 알 수 있습니다. 
 

정다각형은 각 변의 길이가 모두 같은 도형으로, 정다각형의 둘레 = 한 변의 길이 X 변의 수 입니다.

한 변의 길이가 7cm인 정오각형의 둘레를 구하라는 문제가 나오면, 7cm X 5 = 35cm 가 됩니다.



둘레를 공부했으니 넓이를 구하는 방법에 대해 설명드릴게요.
 

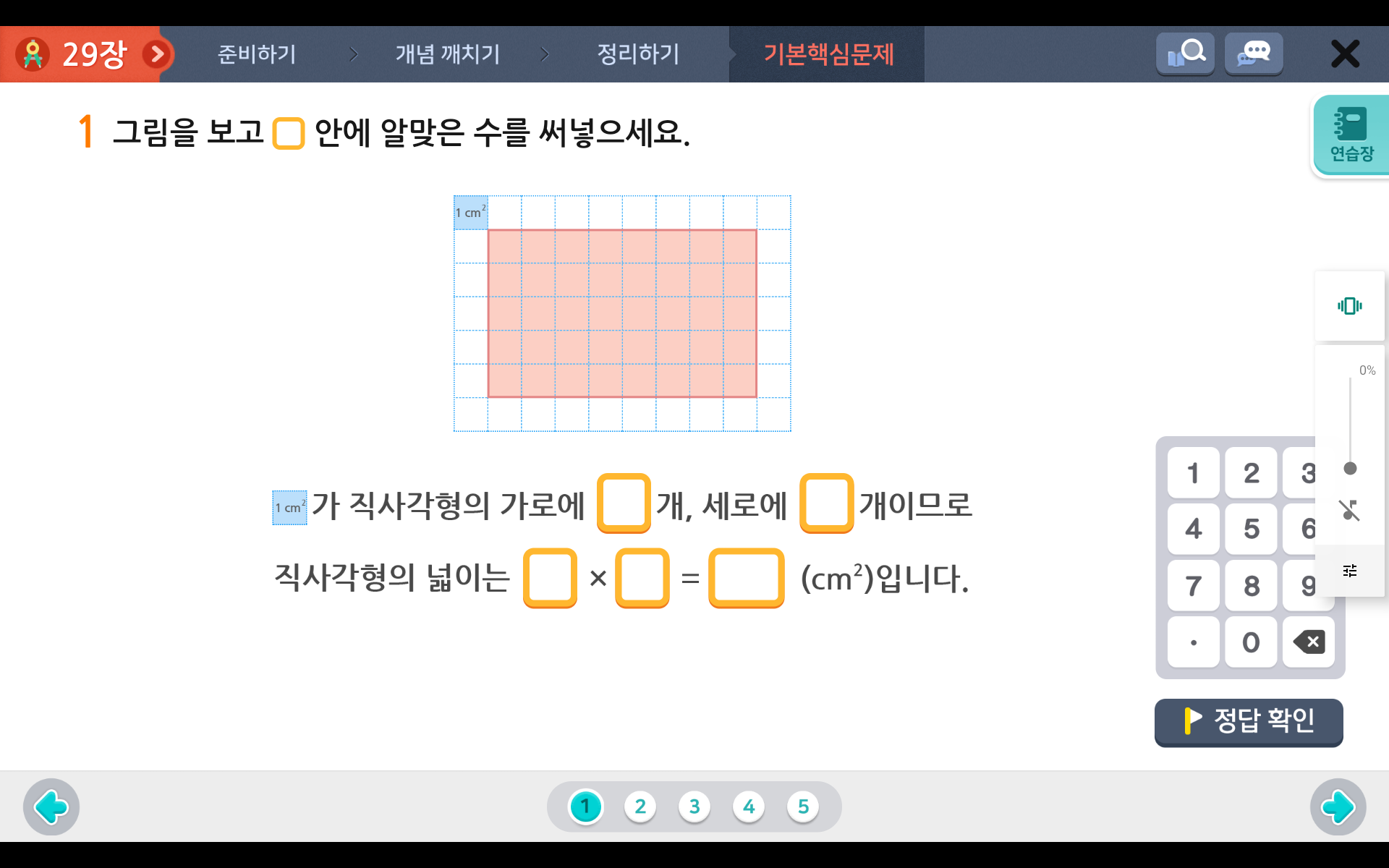
1.직사각형 넓이: 가로 X 세로

직사각형의 넓이는 가로 x 세로로, 가로 2cm와 세로 3cm인 직사각형의 넓이는 2 x 3 =6cm² 입니다.

 

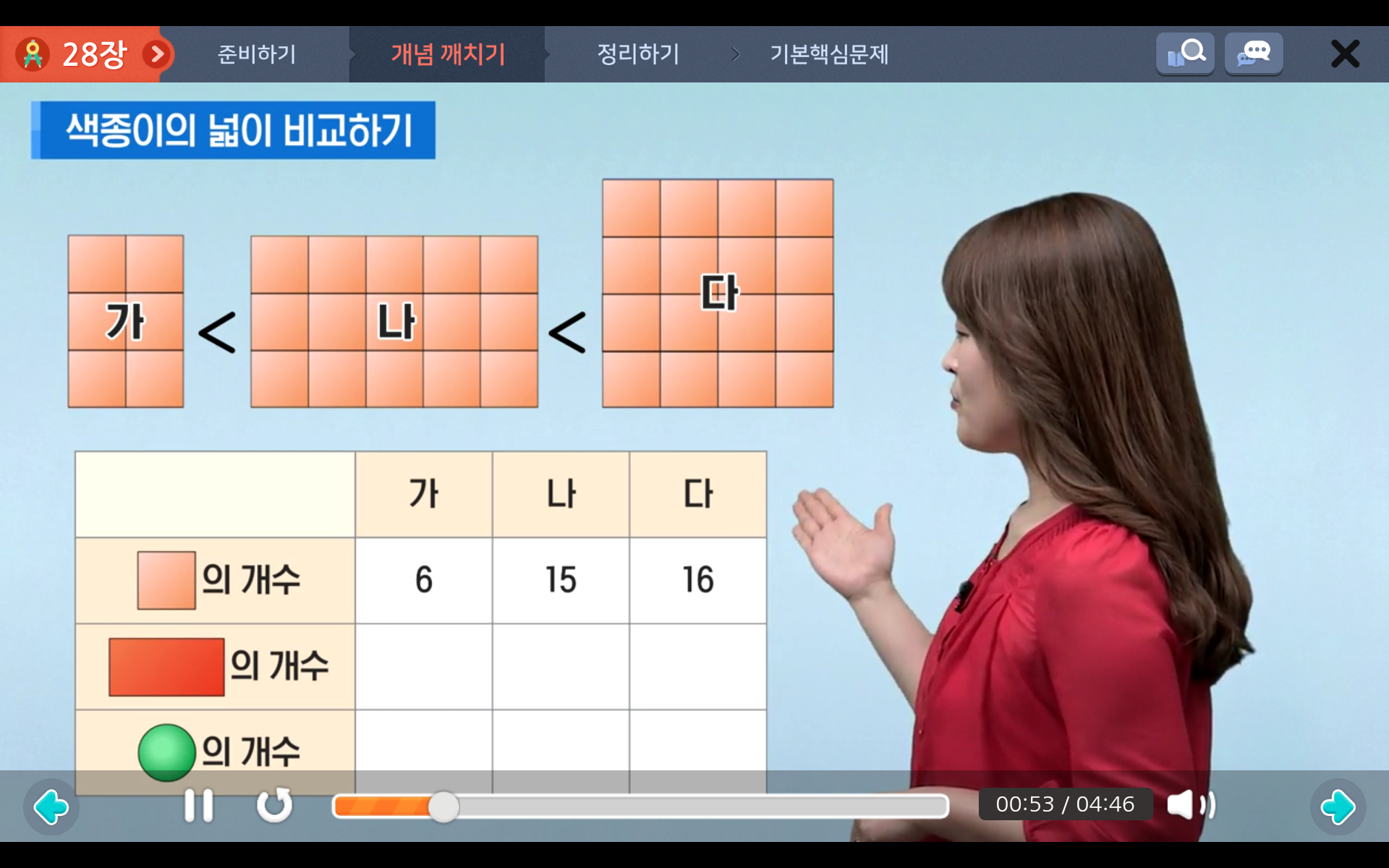
2.정사각형 넓이: 한 변의 길이 X 한 변의 길이

정사각형은 가로와 세로의 길이가 같으며, 한 변의 길이가 6cm인 정사각형의 넓이는 6 x 6 = 36cm²가 됩니다.
 

3.평행사변형의 넓이: 밑변의 길이 X 높이로, 평생사변형에서는 평행한 두 변을 밑변이라고 하고 두 밑변 사이의 거리를 높이라고 합니다.

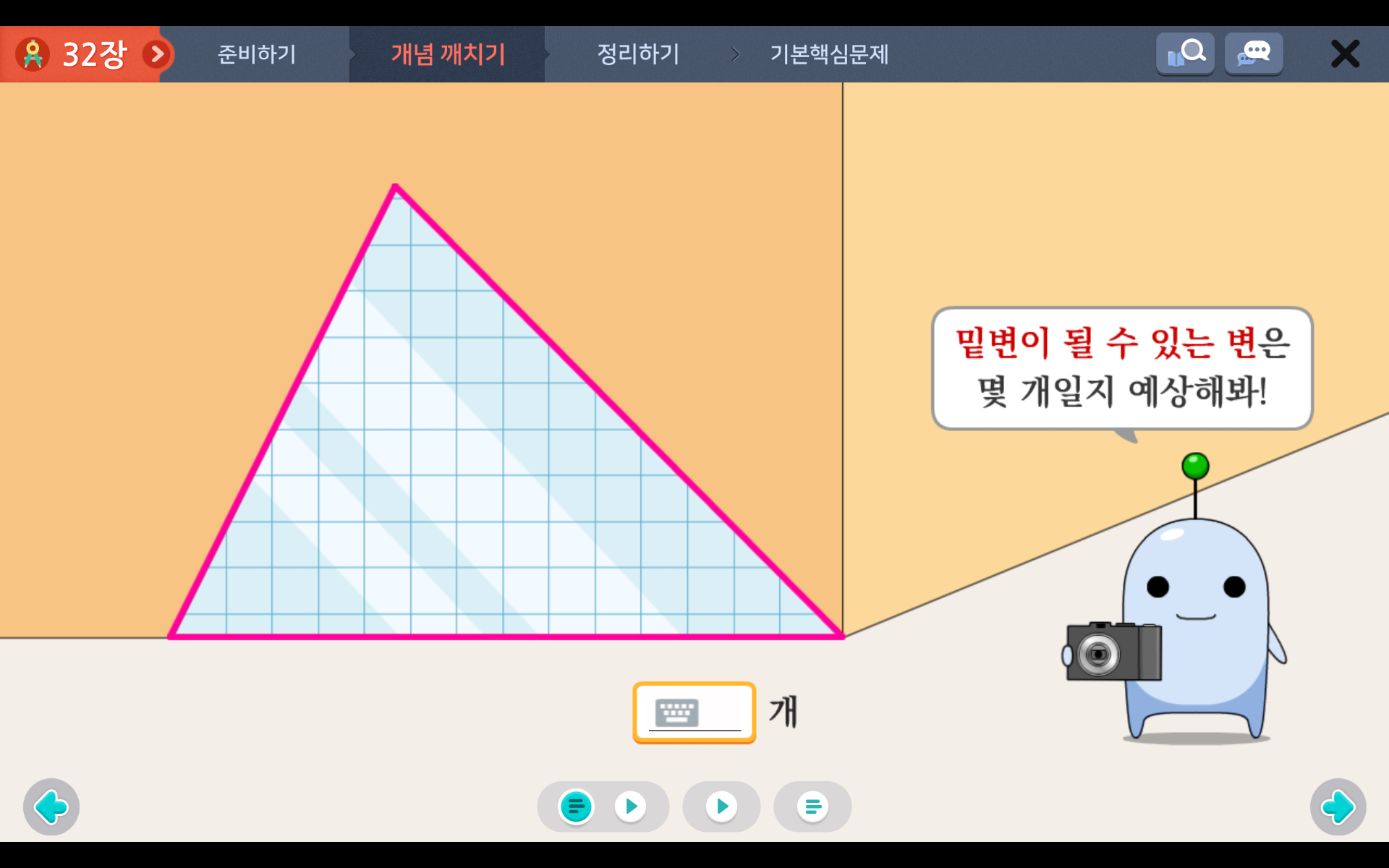
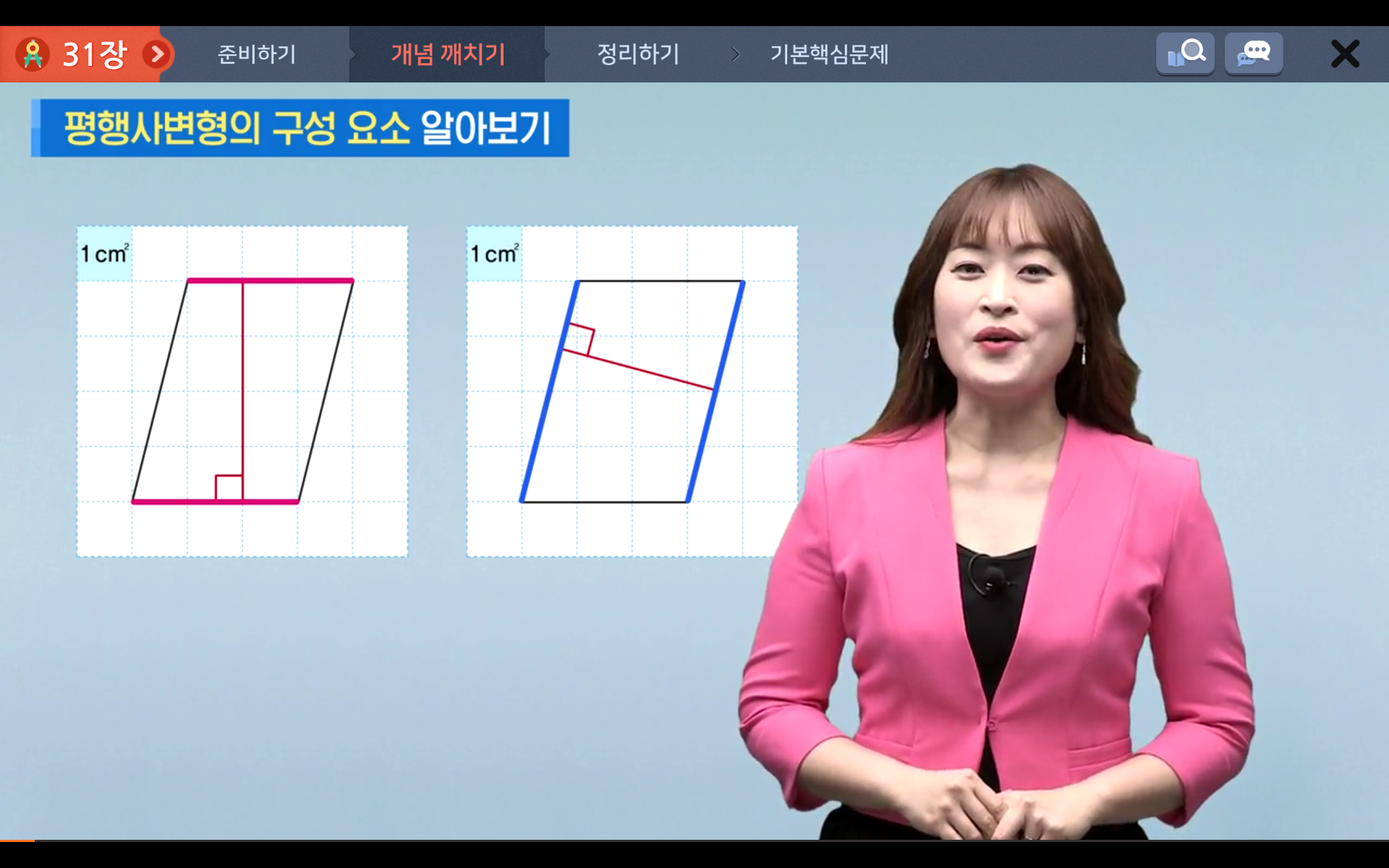4.삼각형의 넓이: 삼각형에서는 어느 한 변을 밑변이라고 하면, 밑변과 마주보는 꼭짓점에서 밑변에 수직으로 그은 선분의 길이를 높이라고 합니다.

삼각형의 넓이는 밑변의 길이 X 높이 ÷ 2 입니다.

다양한 도형의 넓이 구하는 문제 풀기>
 

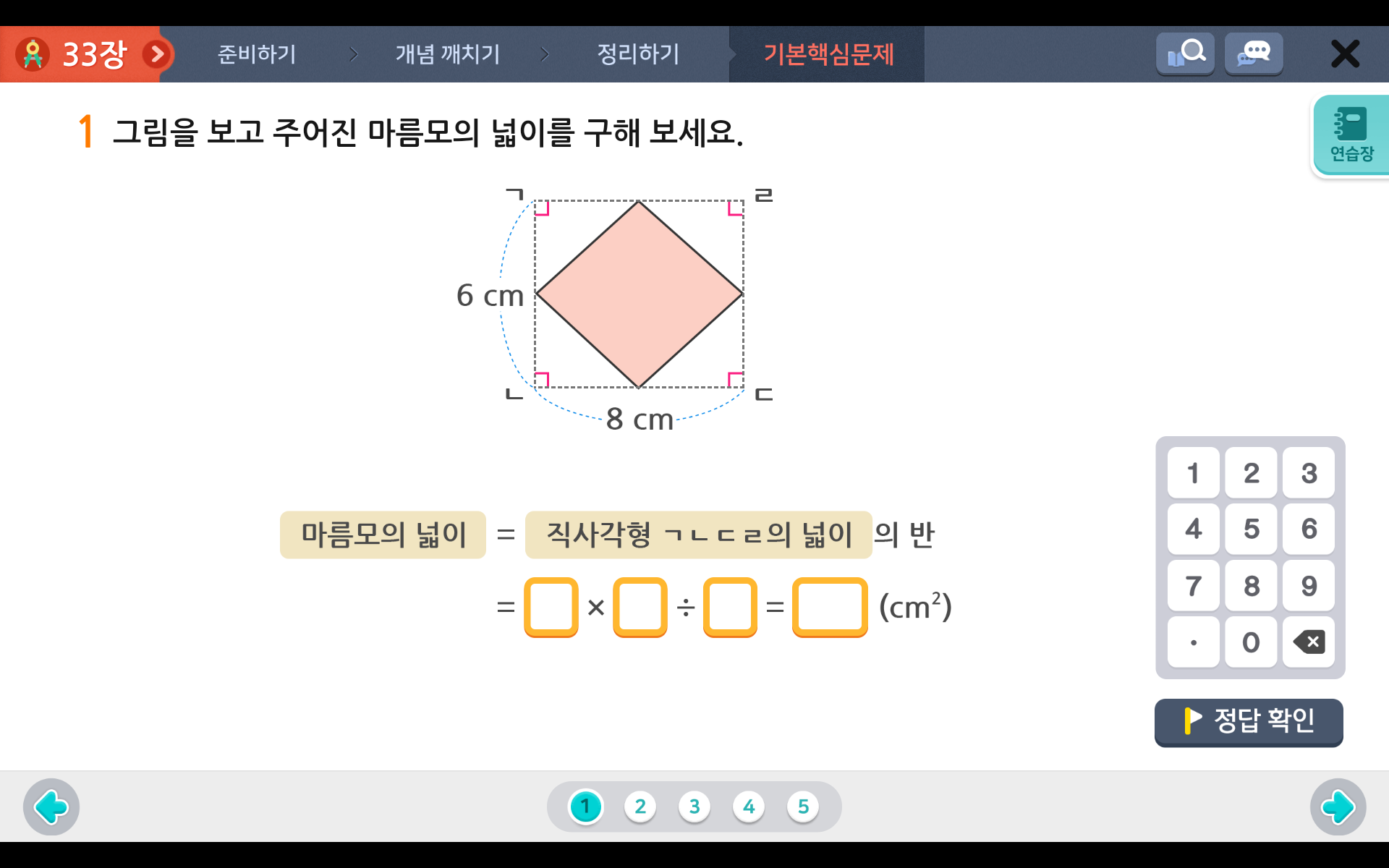
5.마름모의 넓이: 한 대각선의 길이 X 다른 대각선의 길이÷ 2

마름모는 네 변의 길이가 모두 같은 평생사변형으로, 대각선의 길이가 6cm, 8cm인 마름모의 넓이는 6 x 8 ÷ 2 로 24 cm²가 됩니다.

 

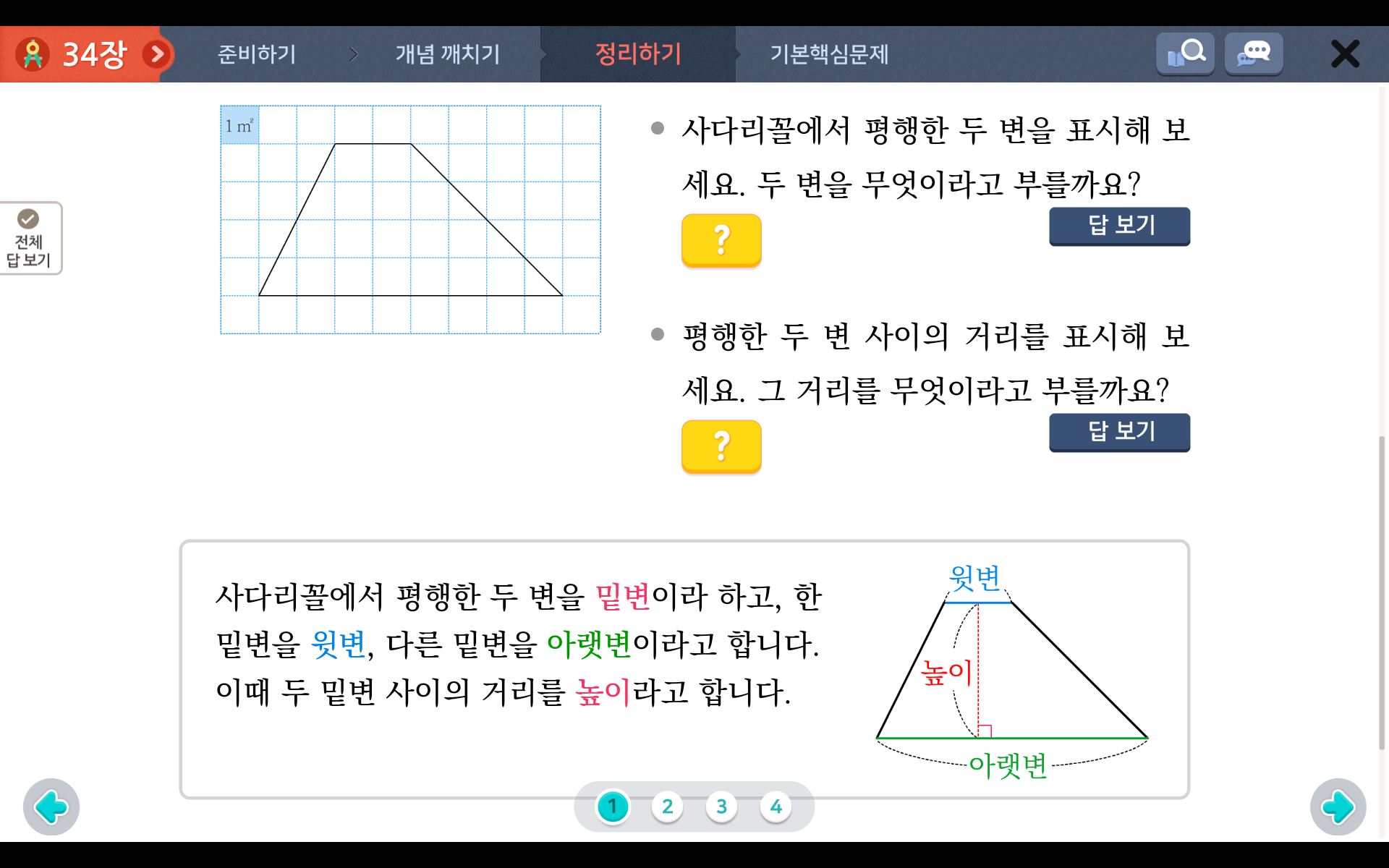
6.사다리꼴의 넓이: (윗변의 길이 + 아랫변의 길이) X높이 ÷ 2 입니다.

사다리꼴은 평행한 변이 있는 사각형, 즉 마주 보는 한 쌍의 변이 서로 평행하는 사각형을 사다리꼴이라고 합니다.




넓이를 구하다보면 cm² 을 접하게 될텐데요! cm만 봤는데 cm²는 뭐지? 라는 궁금증 생기셨었죠?
cm²는 제곱센티미터로 읽으며, 넓이를 나타낼 때 한 변의 길이가 1cm인 정사각형의 넓이를 단위로 사용할 수 있어요!


예시로 설명해드릴게요.
한 변의 길이가 1cm인 정사각형의 넓이를 구한다면, 정사각형의 넓이 공식은 한 변의 길이 X 한 변의 길이이므로 1cm X 1cm 이므로 1cm²가 됩니다.
해당 법칙을 적용하면 1m 인 정사각형의 넓이는 1m² 가 되며 일 제곱미터로 읽으면 됩니다!

도형의 둘레와 넓이는 공식을 어느정도 외워야 문제 풀이가 가능하지만, 많은 문제를 풀다 보면 공식이 자연스레 익혀져 굳이 외우려 노력하지 않아도 문제를 풀게 될 거예요!
다각형의 둘레와 넓이도 역시, 홈런초등 학습기에서 무료로 공부해보세요.

다각형의 둘레와 넓이 다양한 문제 풀기>