안녕하세요. 공부를 좋아하는 습관을 만들어 주는 아이스크림 홈런입니다.
이번 시간에는 5학년 2학기 3단원 합동과 대칭에 대해 알려드리려고 해요.
합동과 대칭에서는 합동의 뜻, 합동인 도형의 성질, 선대칭도형 및 점대칭도형에 대해 배우게 됩니다.
합동의 뜻부터 차근차근 시작해보도록 하겠습니다.
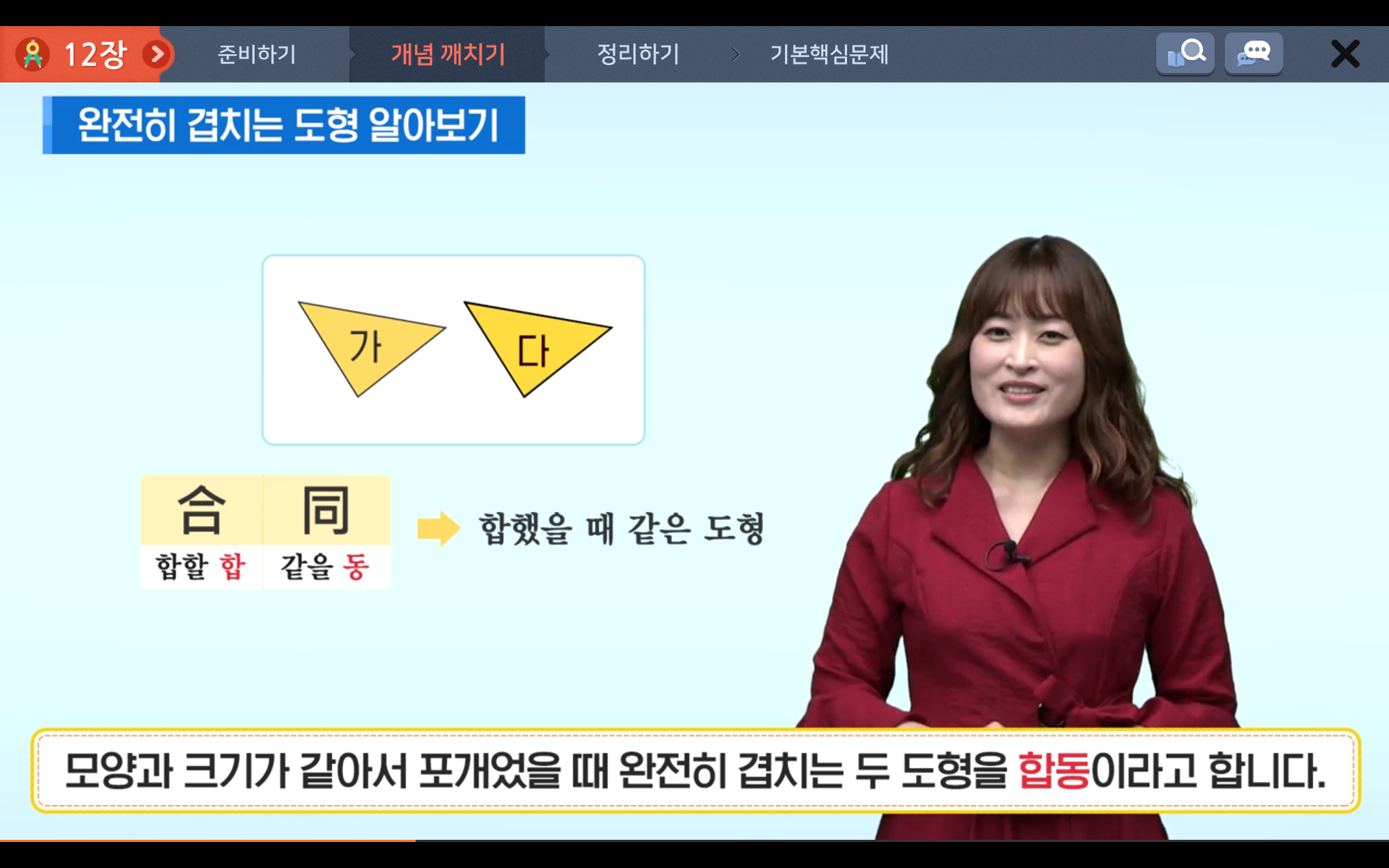
도형의 합동은 모양과 크기가 같아서 포개었을 때 완전히 겹치는 두 도형을 서로 합동이라고 합니다.
모양은 같지만 크기가 다르면 합동이라고 하지 않습니다.
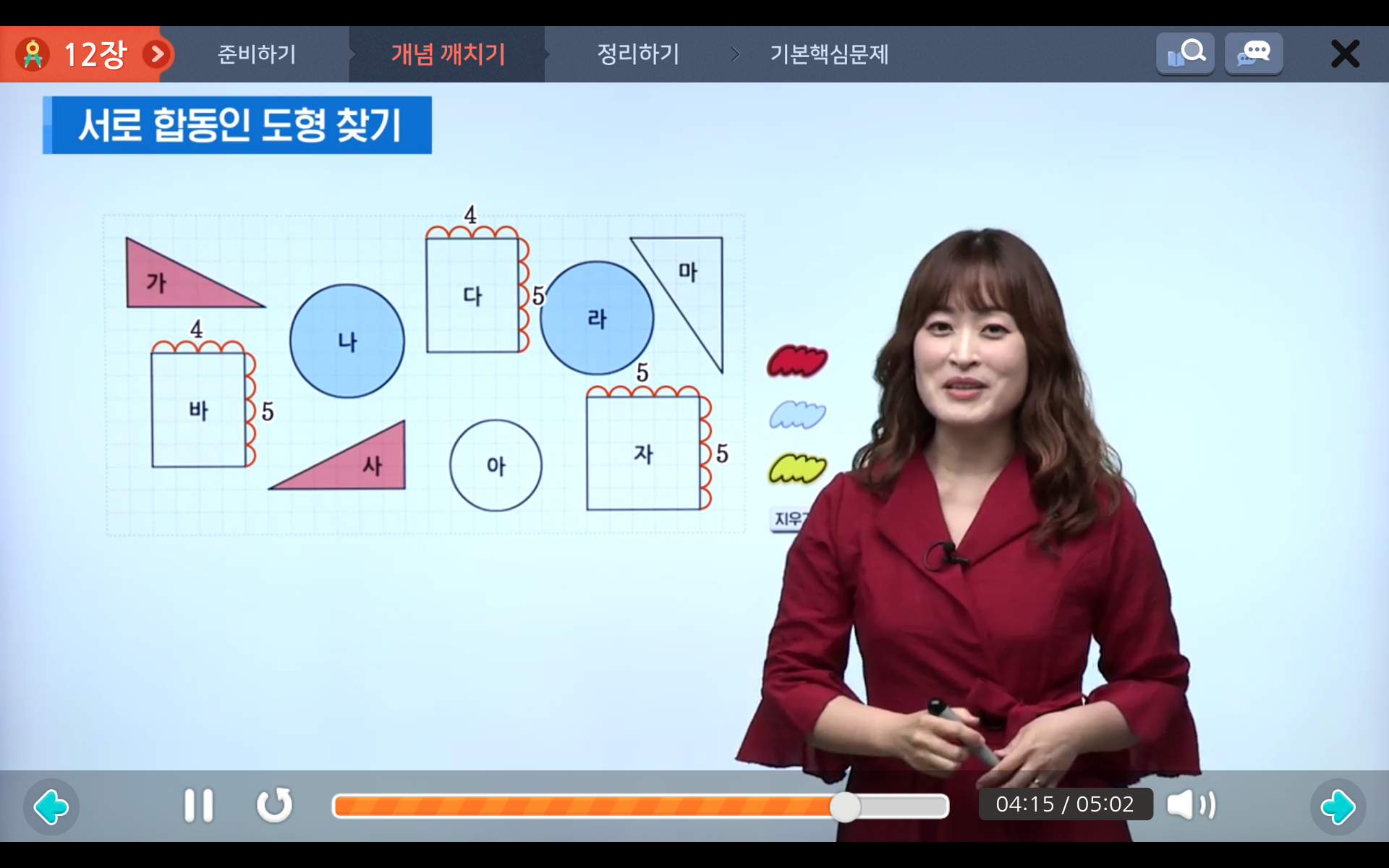
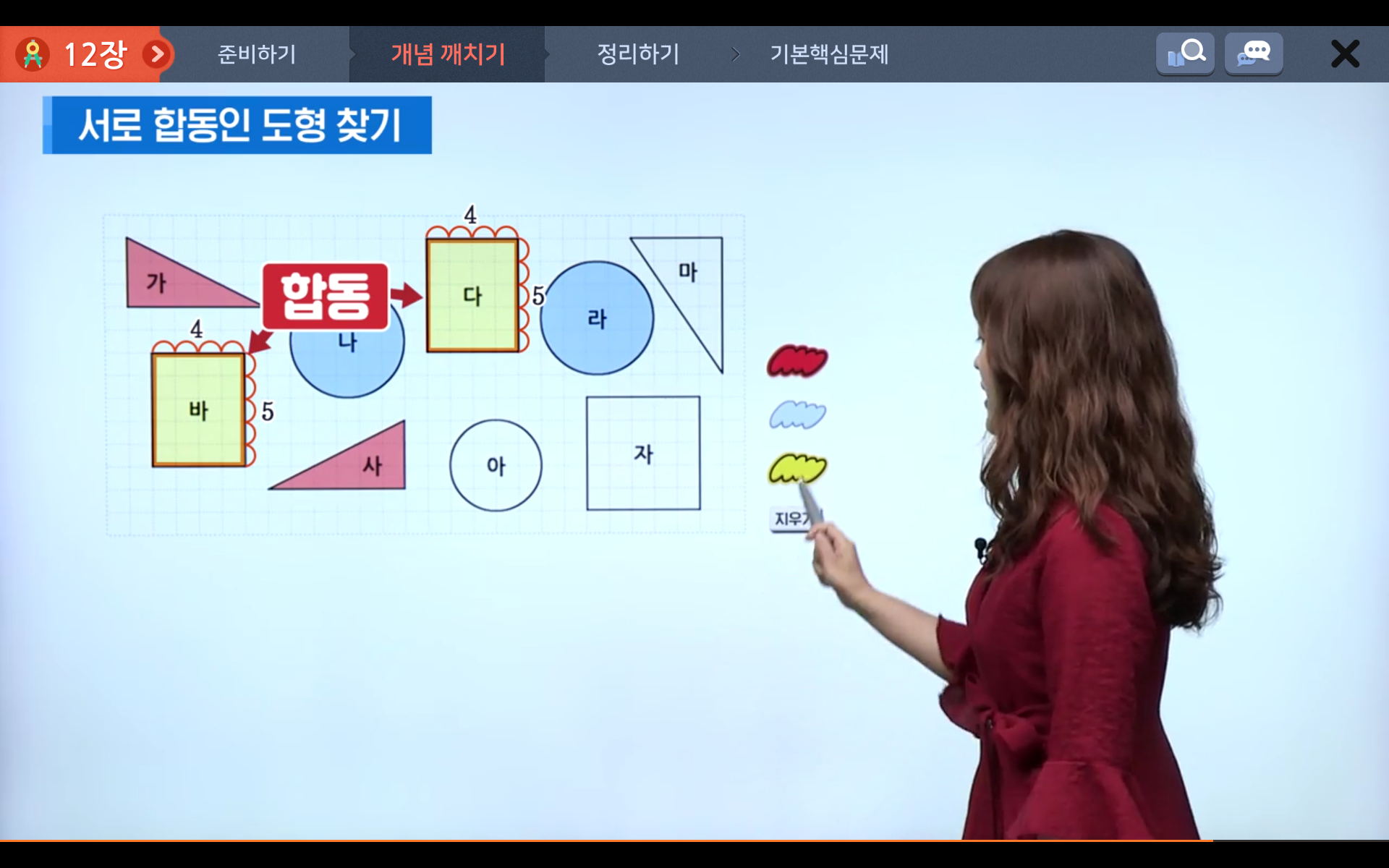
모양과 크기가 같아 완전히 포개지는 두 도형을 합동이라고 하므로,
아래에서 합동인 도형을 찾아보면 가와 사, 나와 라, 다와 바가 됩니다.
 서로 합동인 두 도형을 포개었을 때, 대응점, 대응변, 대응각은 다음과 같습니다.
서로 합동인 두 도형을 포개었을 때, 대응점, 대응변, 대응각은 다음과 같습니다.
1)대응점: 완전히 겹치는 점
2)대응변: 완전히 겹치는 변
3)대응각: 완전히 겹치는 각
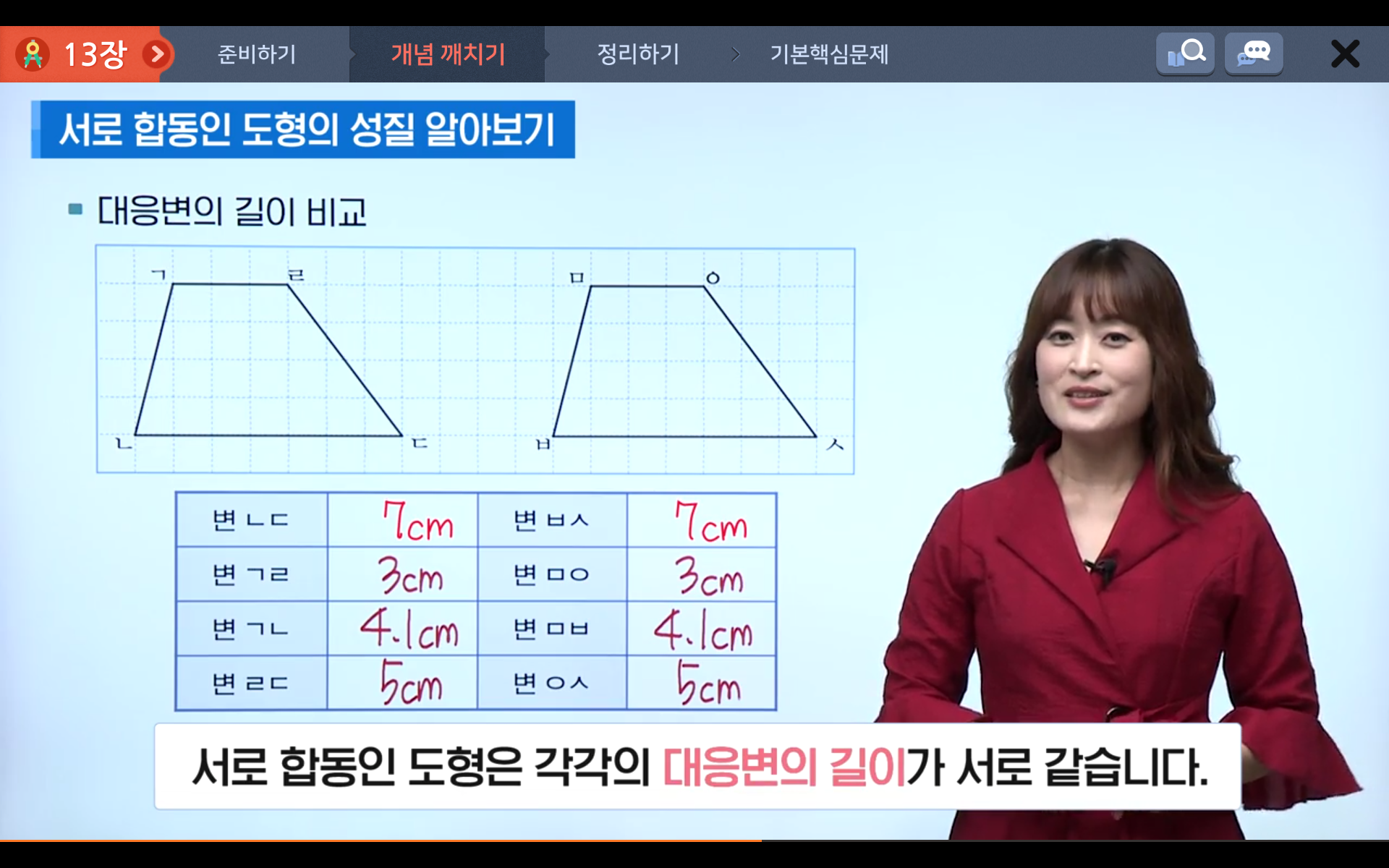
또한, 서로 합동인 도형의 대응변은 길이가 같으며, 대응각 또한 크기가 같습니다.

선대칭도형에 대해 알아보겠습니다.
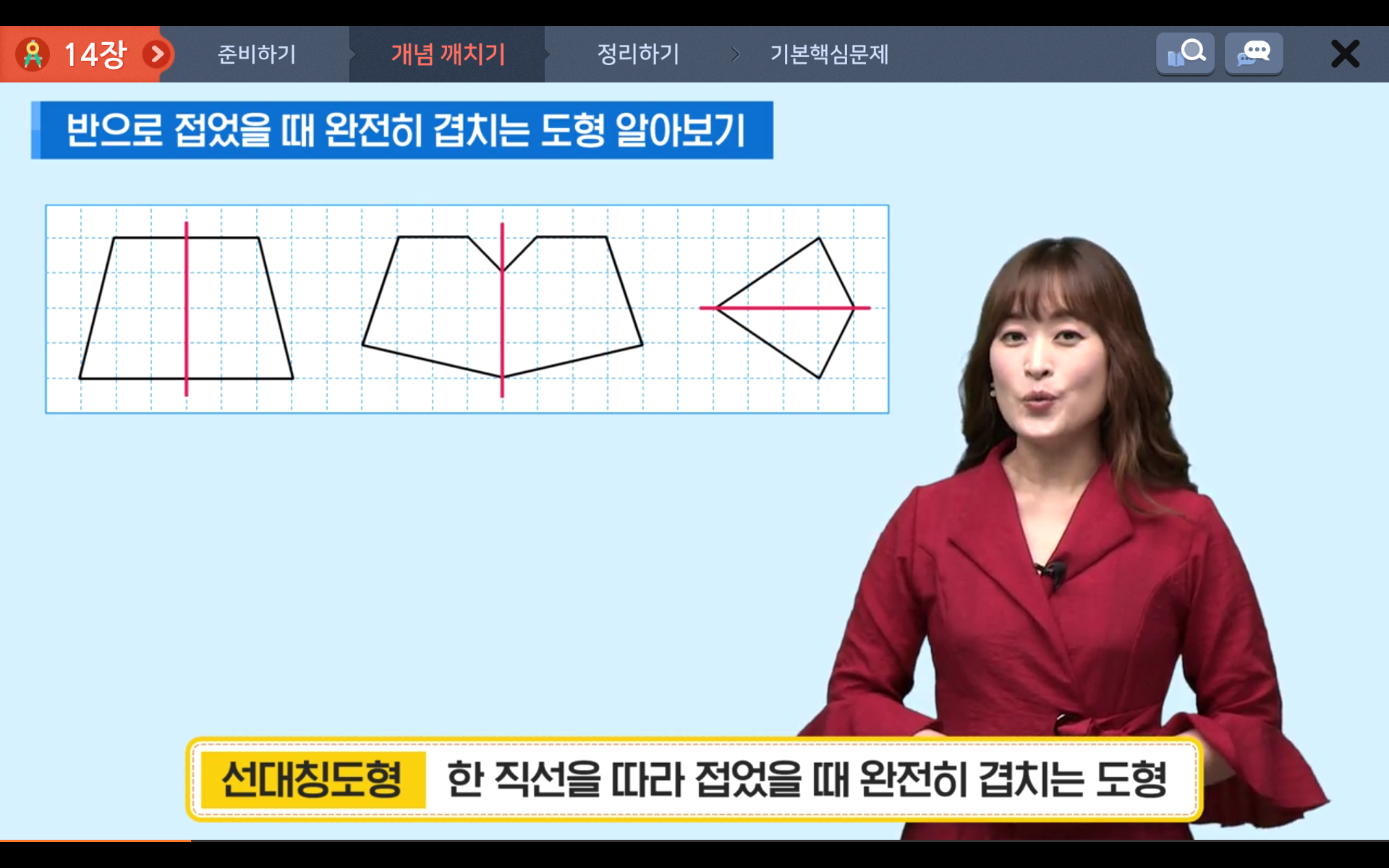
한 직선을 따라 접었을 때 완전히 겹치는 도형을 선대칭도형이라고 합니다.
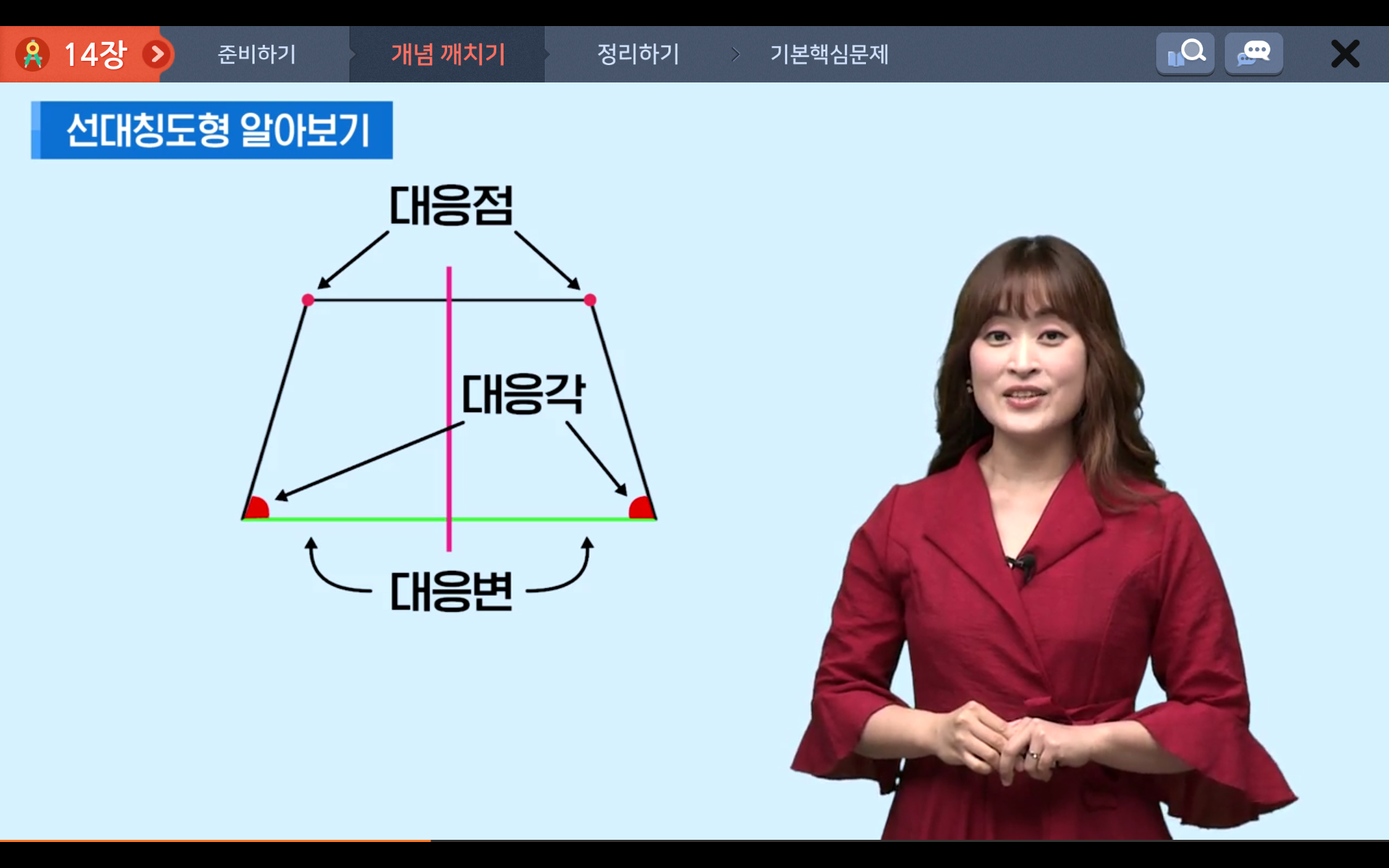
이 때 그 직선을 대칭축이라고 하며, 대칭축을 따라 접었을 때 겹치는 점, 변, 각을 대응점, 대응변, 대응각이라고 합니다,
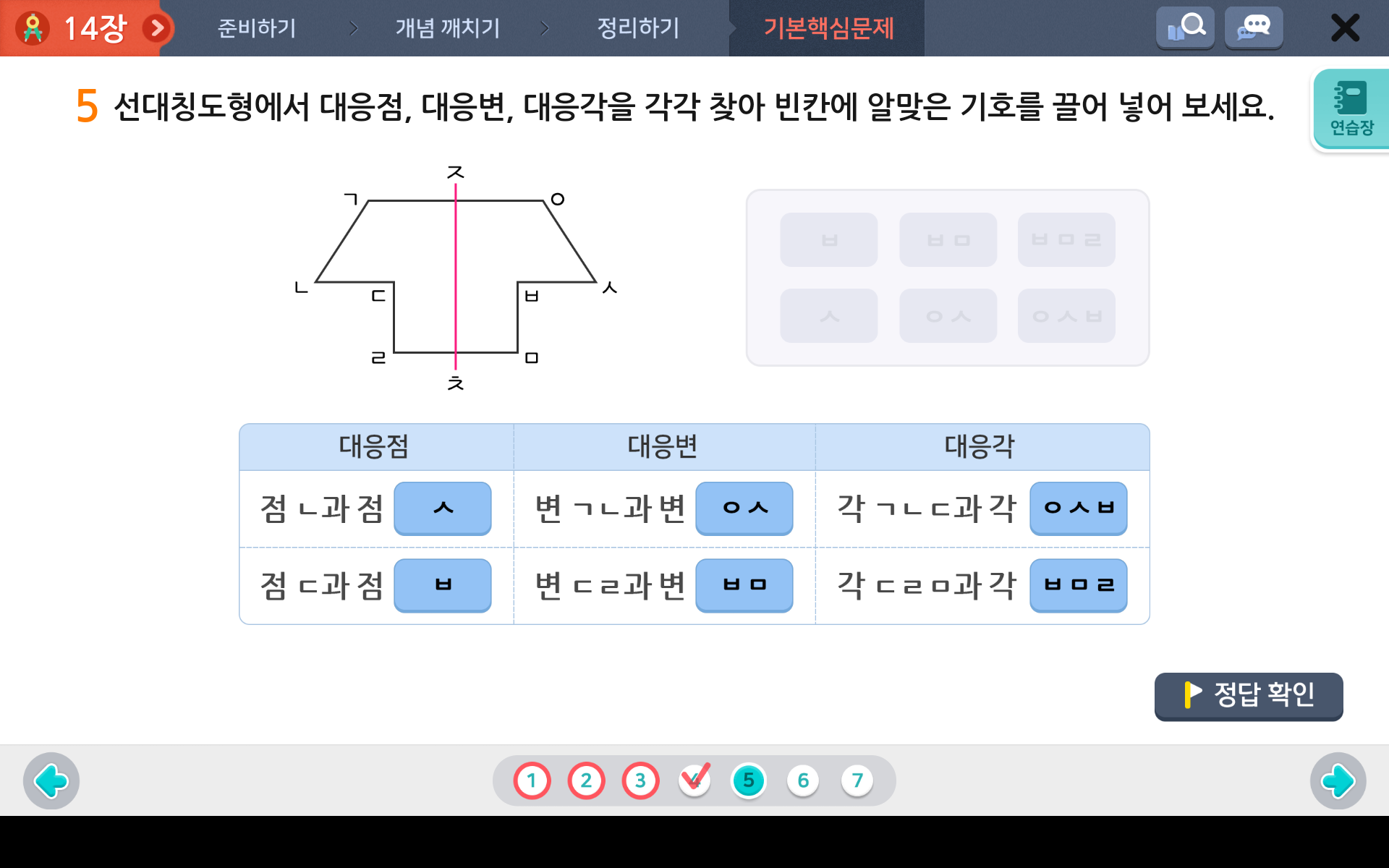
선대칭도형의 대응점, 대응변, 대응각에 대해 알아봤으니 아래 문제를 보면서 각각의 정답을 찾아보도록 해요.
선을 중심으로 대응하는 점, 변, 각을 찾으면 되겠죠?
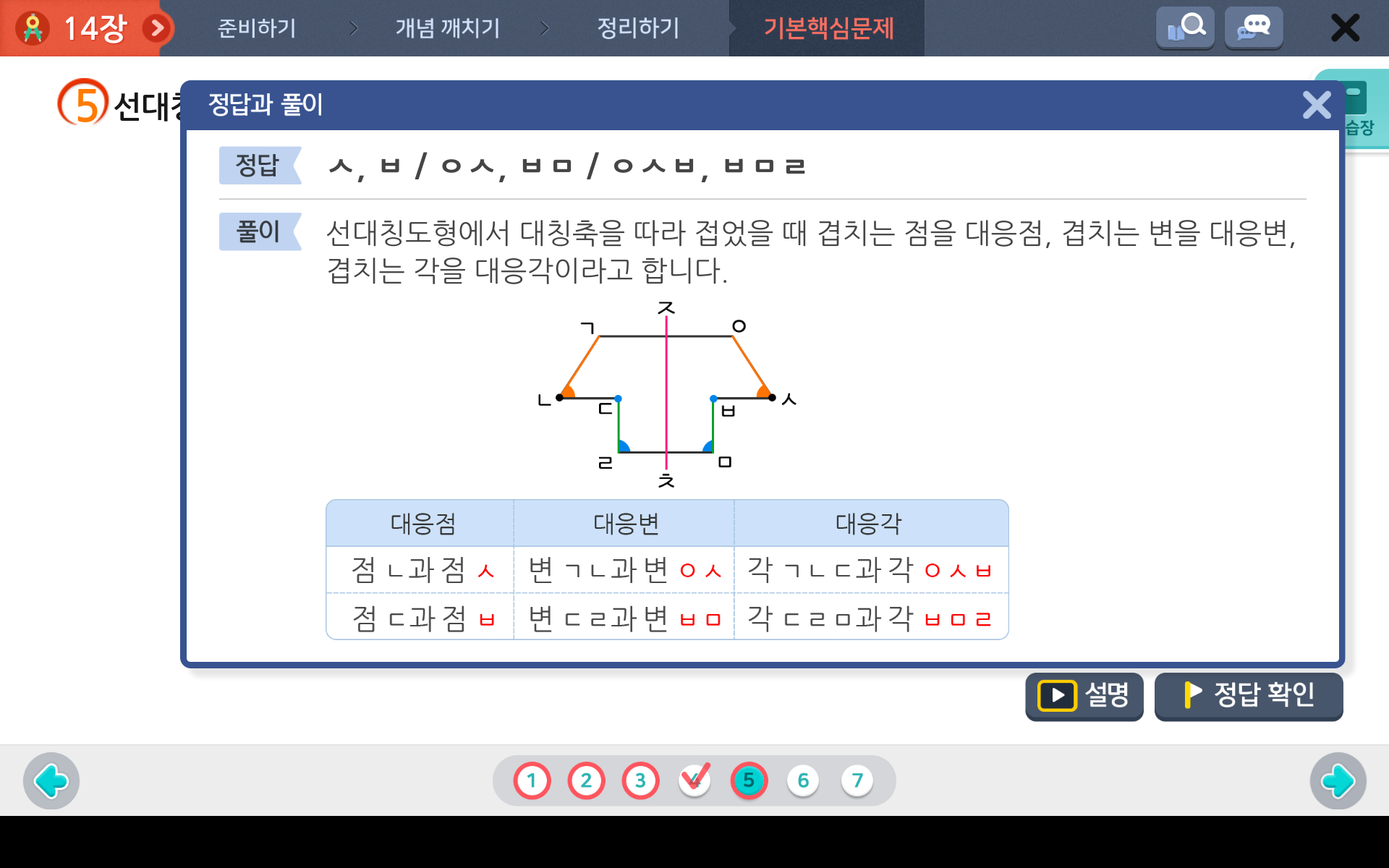
선대칭도형에 대해 배워봤으니 점대칭도형에 대해 알아볼까요?
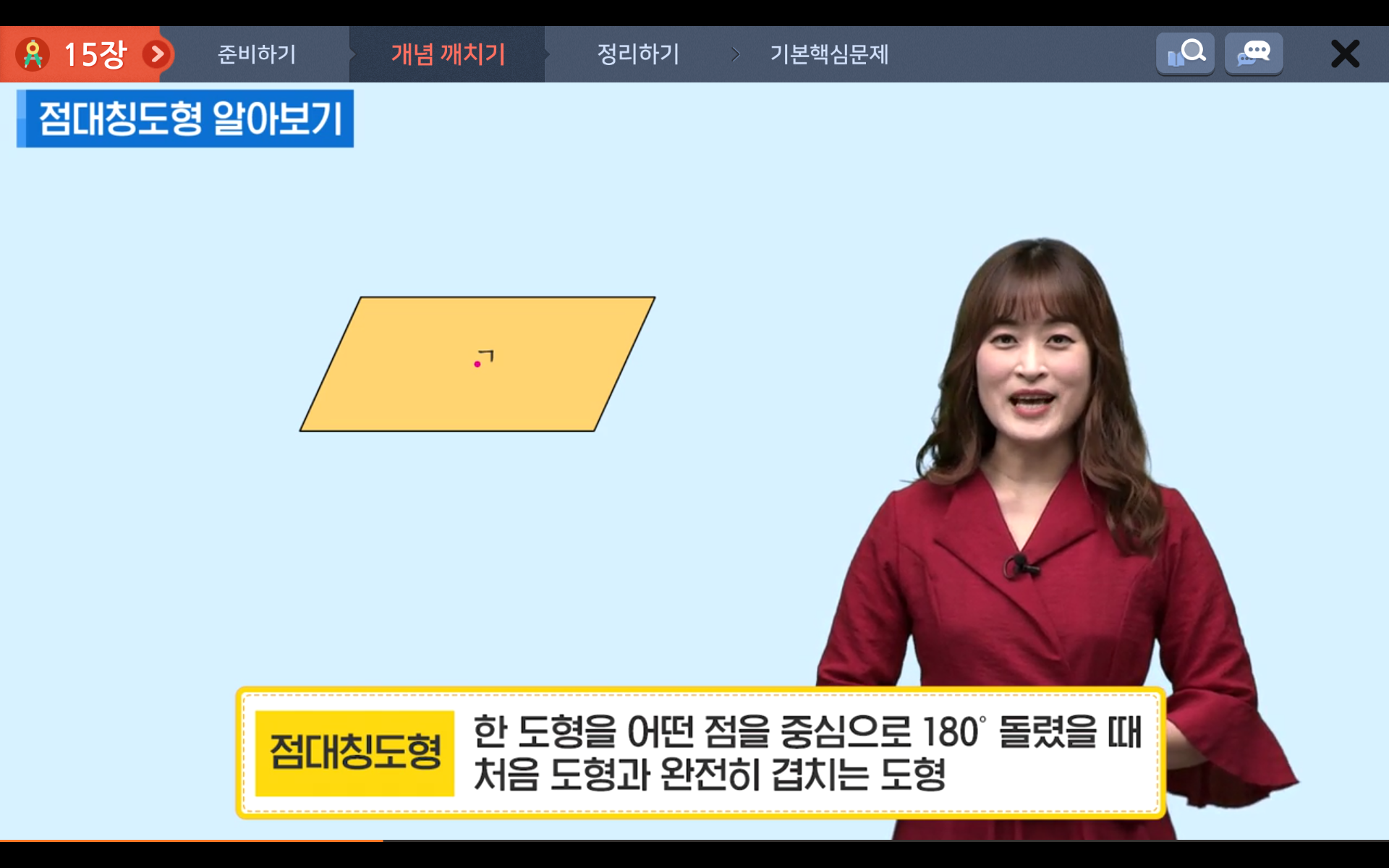
점대칭도형은 한 도형을 어떤 점을 중심으로 180° 돌렸을 때 처음 도형과 완전히 겹치는 도형을 말합니다.

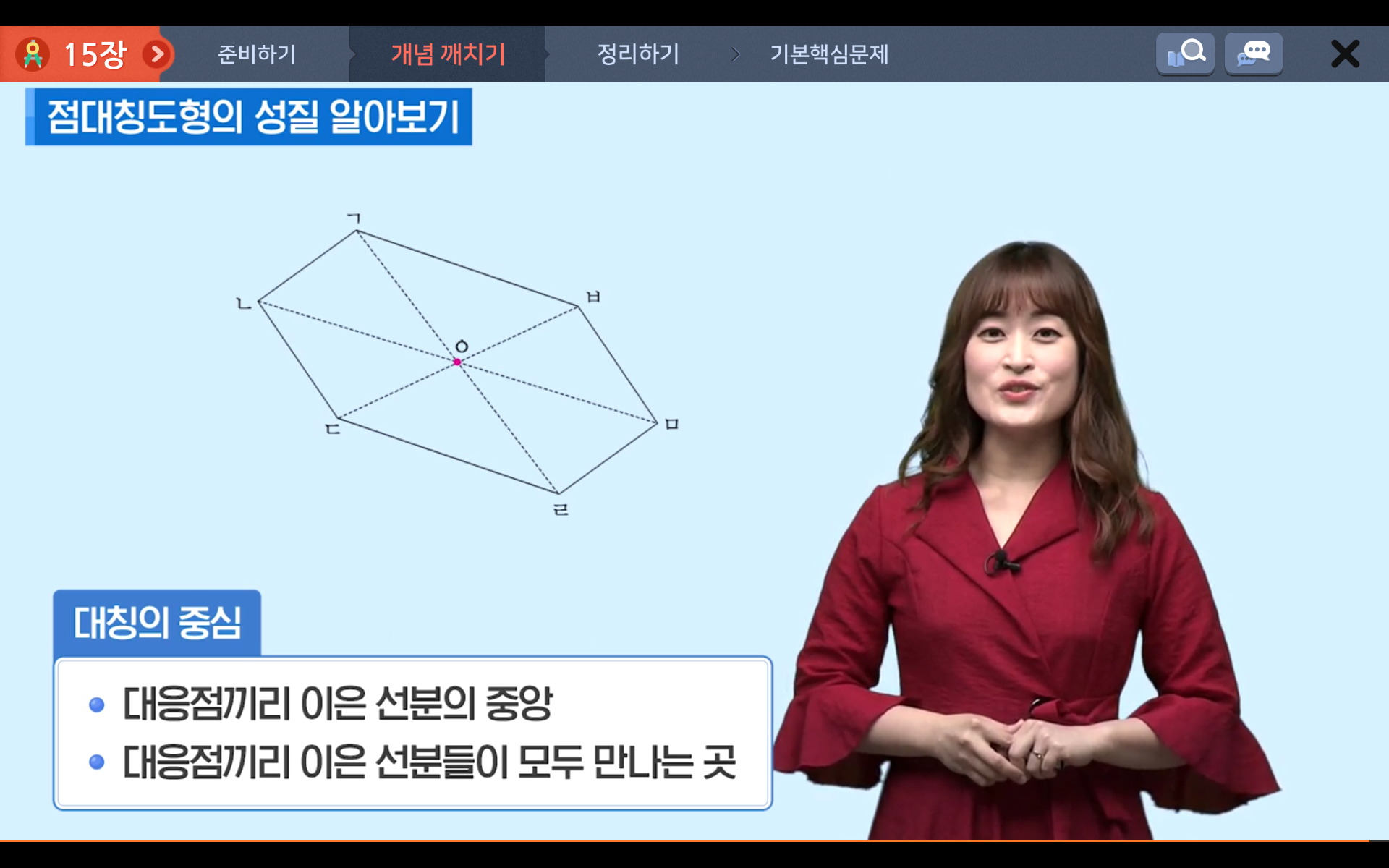
이때 그 점을 대칭의 중심 이라고 합니다.
대칭의 중심은 대응점끼리 이은 선분의 중앙, 대응점끼리 이은 선분들이 모두 만나는 곳을 말합니다.
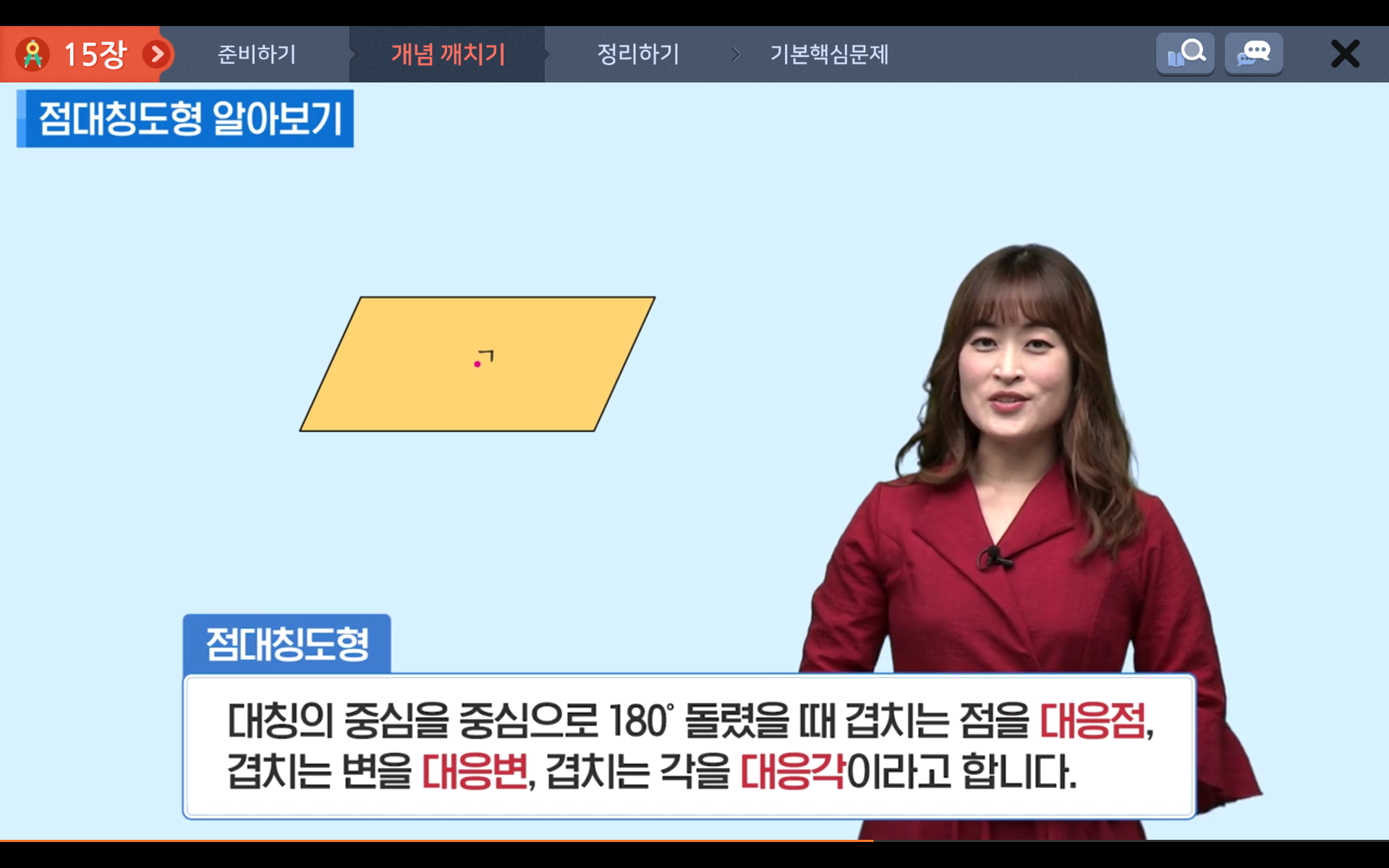
점대칭도형도 마찬가지로 대칭의 중심을 중심으로 180° 돌렸을 때
겹치는 점은 대응점, 겹치는 변은 대응변, 겹치는 각을 대응각이라고 합니다.
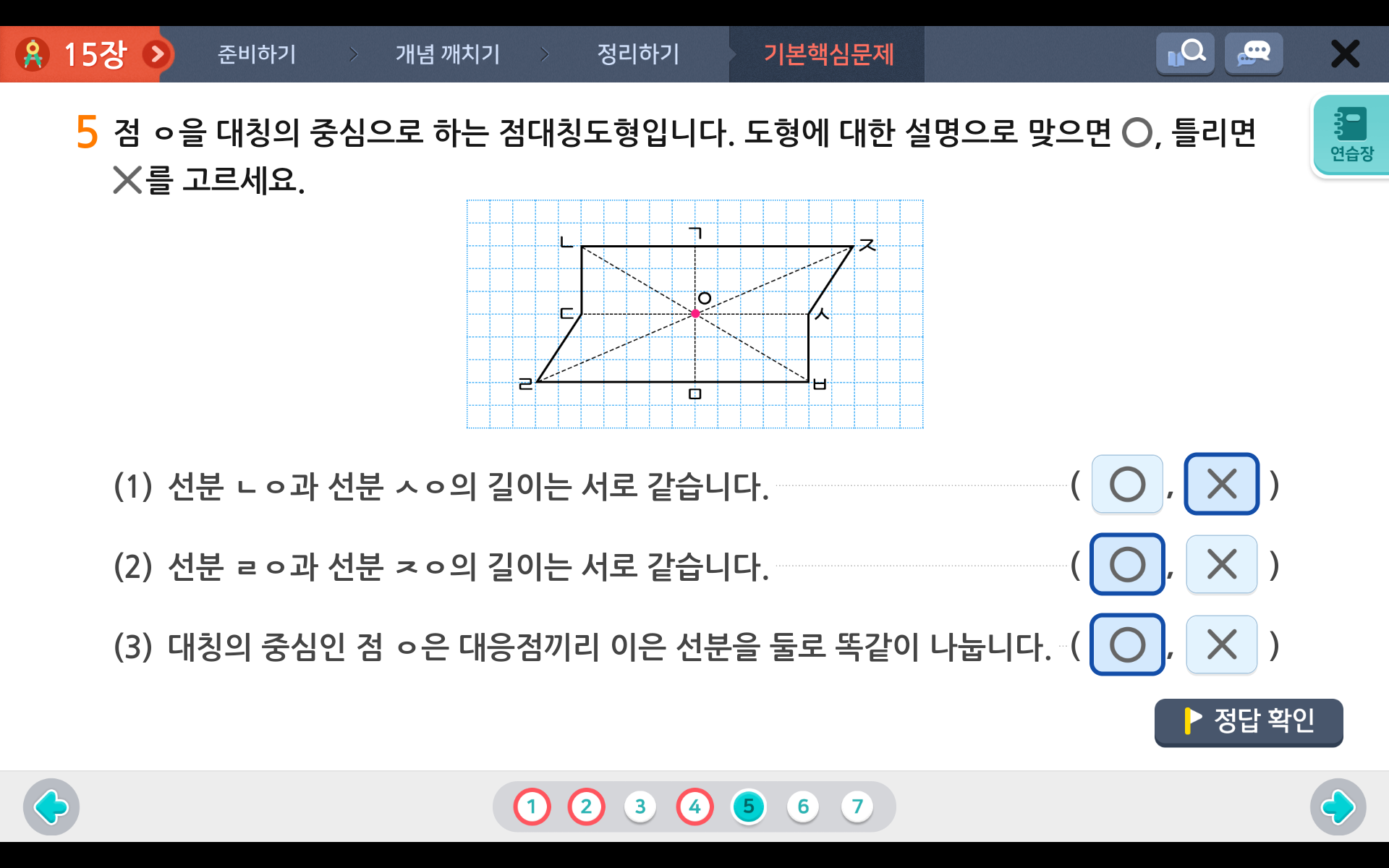
 점대칭도형과 관련된 문제
점대칭도형과 관련된 문제 풀어보고 3단원 합동과 대칭과 관련된 학습 내용 마무리 하도록 하겠습니다.
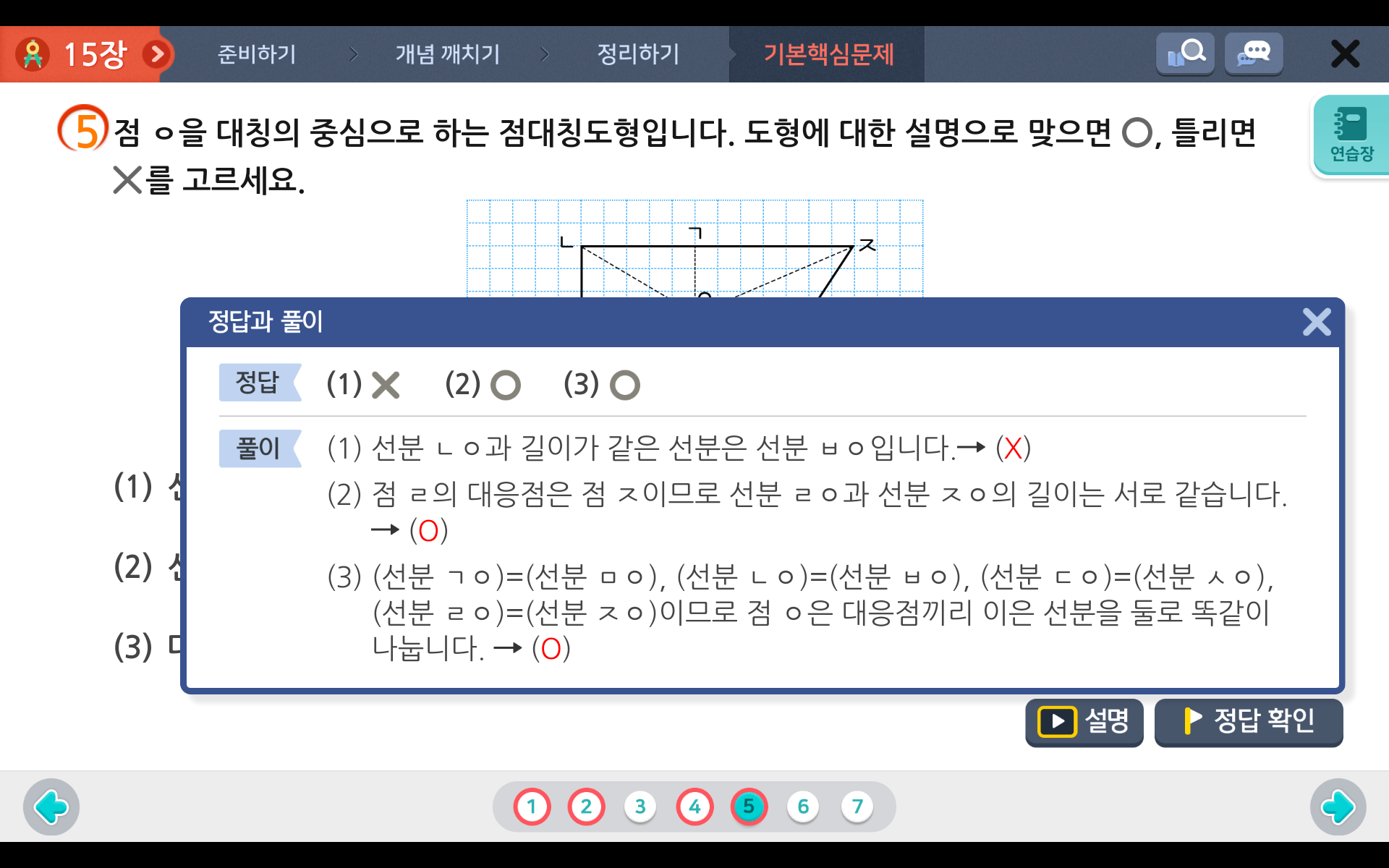
1) 선분 ㄴㅇ과 선분 ㅅㅇ의 길이는 서로 같습니다. > 아니죠? 대응변이 아니므로 길이는 같지 않습니다.
2) 선분 ㄹㅇ과 선분 ㅈㅇ의 길이는 서로 갑습니다. > 대칭의 중점을 기준으로 대응변이므로 길이는 같습니다.
3) 대칭의 중점인 점 ㅇ은 대응점끼리 이은 선분을 둘로 똑같이 나눕니다. > 당연히 정답이 되겠죠?
지금까지 합동과 대칭에 대해 알아봤는데요! 이번 수업 어떠셨나요
3단원 합동과 대칭을 끝으로 5학년 2학기 수학에 관련된 내용을 모두 배워봤는데요.
많은 문제를 풀어보고 싶거나, 배운 내용에 대한 복습이 필요하다면 지금 홈런 무료체험을 시작해보세요!
홈런 무료체험 바로가기>















